Backdoor CTF from IIT Roorkee

A very nice CTF organized by the Info Sec club at IIT Roorkee. A very high quality set of challenges in all categories.

Beginner

Mini RSA

The key elements of the challenge are that there is a custom implementation of pow(a,b,n) and seemingly unrelated value derived by private primes p and q are being leaked. More about this in Mini_RSA_v2

KEY_SIZE = 512
RSA_E = 3

# equivalent to pow(a, b, n)
def fast_exp(a, b, n):
    output = 1
    while b > 0:
        if b & 1:
            output = output * a % n
        a = a * a % n
        b >>= 1 
    return output    

# returns   pow(p, pow(q, a_, phi), n) + pow(q, pow(p, b_, phi), n)
def check(p, q, n):
    a_ = random.randint(1, 100)
    b_ = random.randint(1, 100)
    s = fast_exp(p, fast_exp(q, a_, (p - 1) * (q - 1)), n)
    t = fast_exp(q, fast_exp(p, b_, (p - 1) * (q - 1)), n)
    result = s + t
    print(result)       # s + t is leaked

# The flag is encrypted and the ciphertext, along with the modulus N is provided

We see that the public exponent is very small, just 3. So, if the plaintext is small enough that

$P^e\mod{N} := P^3$, which happens when $P^3 < N$

Let’s test it.

from Crypto.Util.number import long_to_bytes
import gmpy2

# from output.txt
st=24986288511406610689718446624210347240800254679541887917496550238025724025245366296475758347972917098615315083893786596239213463034880126152583583770452304
c=5926440800047066468184992240057621921188346083131741617482777221394411358243130401052973132050605103035491365016082149869814064434831123043357292949645845605278066636109516907741970960547141266810284132826982396956610111589
n=155735289132981544011017189391760271645447983310532929187034314934077442930131653227631280820261488048477635481834924391697025189196282777696908403230429985112108890167443195955327245288626689006734302524489187183667470192109923398146045404320502820234742450852031718895027266342435688387321102862096023537079

# find the cuberoot as E=3.
pt,found = gmpy2.iroot(c, 3)
if (found):
    pt = int(pt)
    print(pt)
    print(long_to_bytes(pt))      # b'flag{S0_y0u_c4n_s0lv3_s0m3_RSA}'

Just taking the cuberoot of the ciphertext gives us the flag. And, we did not have to touch that strange-looking s+t value

Mini RSA_v2

This is essentially the same challenge as the previous Mini RSA, with the exponent changed from 3 to 65537. So, we can disregard the loophole that allowed us to crack the first problem.

I solved this challenge intuitively by using small primes to figure out that the provided value s+t == p+q. From that point onwards, the solution is straight-forward.

st = ...    # s+t, which is equal to p+q
c  = ...
n  = ...
phi = n - st + 1    # (p-1)(q-1) = pq - (p+q) + 1 = n - st + 1
d = pow(RSA_E, -1, phi)
print(long_to_bytes(pow(c, d, n)))      # b'flag{I_4m_5tuck_0n_Th3_pl4n3t_Eg0_s4ve_M3}'

However, the reason as to why s+t == p+q is an interesting one. Thanks to ConnorM, Robin and grhkm on the Cryptohack discord for helping me understand some of the concepts.

$$ Given: \boxed {s + t = p^{(q^a \mod \phi)} + q^{(p^b \mod \phi)} \pmod n}\\ \quad{}\\ \text{ We will show: }\\ \bf{s + t} \overset{!}{=} \bf{p + q}\\ \quad\\ \implies {{(q^a \mod \phi)} = {(p^b \mod \phi)} = 1} $$

$$ \text{Proof:} \notag\\ \begin{align} \text{Consider: }s &= p^{(q^a \mod \phi)} \pmod n \notag \\ q^a \mod \phi &= x(p-1)(q-1) + q^a \notag \\ \text{Let k}&= x(p-1) \notag \\ s &= p ^ {k (q-1) + q^a} \pmod n \notag \\ \because \text{n = p * q, and to apply CRT,}& \notag \\ \text{consider cases} \mod p \text { and} \mod q & \notag \\ s \mod p &= p ^ {k (q-1) + q^a} \pmod p = 0 \\ s \mod q &= p ^ {k (q-1) + q^a} \pmod q \notag \\ &= {p ^ k} ^ {(q-1)} \cdot p ^ {q^a} \pmod q \notag \\ \text{From Fermat’s Little Theorem, }x^{(y-1)} &\equiv 1 \pmod y \notag \\ \therefore s \mod q &= 1 \cdot p ^ {q^a} \pmod q \notag \\ &= p ^ {q^a} \pmod q \notag \\ \because p \text{ and } q \text{ are prime numbers, } \notag \\ \text{Case: a = 1}, \quad s \mod q &= p ^ q \pmod q \notag \\ & = p ^{(q-1)} \cdot p \pmod q \notag \\ & = p \pmod q \notag \\ \text{Case: a = k+1}, \quad s \mod q &= p ^{q^{(k+1)}}\pmod q \notag \\ & = {p ^{q^k * q}} \pmod q \notag \\ & = {(p ^{q^k})}^q \pmod q \notag \\ & = {(p ^{q^k})}^{(q-1)} \cdot {(p ^{q^k})} \pmod q \notag \\ & = {p ^{q^k}} \pmod q \notag \\ & \implies \text{equal to Case: a = k} \notag \\ \therefore \underset{a= n}{(s \mod q)} = \underset{a= n-1}{(s \mod q)} &\cdots = \underset{a= 1}{(s \mod q)} = p \mod q \notag \\ \text{Thus by induction: }\quad\forall{a}, \quad s \mod q & = p \pmod q \\ \quad \notag\\ \text{From (1), } {s \mod p} &= 0 \pmod p \notag \\ \tag*{from (1) and (2)}\therefore s \mod (p*q)= s\mod n &\equiv p \pmod n \notag \\ &= p \notag \\ \quad \notag\\ \text{By the same logic, }t\mod n &\equiv q \pmod n \notag \\ &= q \notag\\ \tag{Q.E.D}\therefore \bf{s + t} &= \bf{p + q}\\ \end{align} $$

Indecipherable-image-or-is-it?

We are given a PNG image.

Examine the image file using zsteg
There are 5808 extra bytes at the end of the file. These have magic bytes showing it is a ZIP file.
The LSB 1 bit array gives us a text : keka{1b0asx2w_hbin9K_Ah_6xwm0L}
Extracting and expanding the ZIP file gives us a jpeg image : SECRET/images.jpeg
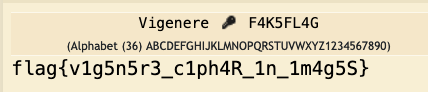
Running stegseek on this JPEG image with the rockyou wordlist, gives us a small text file with F4K5FL4G
Use the Vigenere decoder with the Key:= F4K5FL4G and the ciphertext:=keka{1b0asx2w_hbin9K_Ah_6xwm0L} gives us the flag.

During the competiion, I solved all but the last step, which was a bit guessy, IMO. Or, perhaps it is a skills issue :)

% zsteg cutie.png b1,r,lsb,xy  
[?] 5808 bytes of extra data after image end (IEND), offset = 0xa6ea
extradata:0         .. file: Zip archive data, at least v2.0 to extract
    00000000: 50 4b 03 04 14 00 00 00  08 00 6b 7e 84 57 bd 7e  |PK........k~.W.~|
    00000010: 24 68 2a 16 00 00 b1 16  00 00 12 00 00 00 53 45  |$h*...........SE|
    00000020: 43 52 45 54 2f 69 6d 61  67 65 73 2e 6a 70 65 67  |CRET/images.jpeg|
    00000030: 9d 97 55 58 14 5e b7 c6  07 86 8e 21 04 a4 87 8e  |..UX.^.....!....|
    00000040: a1 1c 42 42 86 51 84 41  40 44 62 00 49 29 89 21  |..BB.Q.A@Db.I).!|
    00000050: a5 41 40 52 41 42 1a e9  ee 90 ee 52 60 28 e9 18  |.A@RAB.....R`(..|
    00000060: 40 5a 3a 44 52 6a f8 f8  7f cf 89 9b 73 71 ce 79  |@Z:DRj......sq.y|
    00000070: f7 e5 bb 9e fd bc bf bd  d6 c5 da b7 98 db 65 00  |..............e.|
    00000080: a5 0a 42 19 01 c0 c1 01  00 70 ee 0e e0 76 1e f0  |..B......p...v..|
    00000090: 14 40 4c 40 48 44 48 40  4c 44 48 44 42 42 4c 4a  |.@L@HDH@LDHDBBLJ|
    000000a0: 4e 47 41 4e 46 46 ce 44  43 4b 49 c7 c6 c2 c1 c1  |NGANFF.DCKI.....|
    000000b0: c6 02 06 73 f1 89 0b 72  f1 40 79 c1 60 21 98 10  |...s...r.@y.`!..|
    000000c0: 54 42 52 46 46 86 53 00  ae 00 97 7a 2a 2e 2d 23  |TBRFF.S....z*.-#|
    000000d0: f9 cf 25 38 24 24 24 e4  64 e4 8c 14 14 8c 92 dc  |..%8$$$.d.......|
    000000e0: 60 6e c9 ff b3 6e 3b 01  54 44 00 6f c0 2c 10 87  |`n...n;.TD.o.,..|
    000000f0: 03 80 4b 85 03 a4 c2 b9  ed 06 80 ef 72 e2 e3 fc  |..K.........r...|

b1,r,lsb,xy         .. text: "keka{1b0asx2w_hbin9K_Ah_6xwm0L}"

% stegseek SECRET/images.jpeg /input/tools/wordlists/rockyou.txt 
StegSeek 0.6 - https://github.com/RickdeJager/StegSeek

[i] Found passphrase: "easyone"          
[i] Original filename: "a.txt".
[i] Extracting to "images.jpeg.out".

% cat images.jpeg.out
F4K5FL4G

Finally, put the encoded flag and the key F4K5FL4G in to Vigenere decoder on dcode.fr and adjust the alphabets to get the right flag.

Crypto

Something in Common

flag = "This flag has been REDACTED"
moduli = "This array has been REDACTED"     # Array of pre-selected modulii

m = bytes_to_long(flag.encode())
e = 3
remainders = [pow(m,e,n) for n in moduli]   # Residuals or congruences

f = open('output.txt','w')
for i in range(len(moduli)):
    f.write(f"m ^ e mod {moduli[i]} = {remainders[i]}\n")   # we are given residuals and the corresponding modulus
f.write(f"\ne = {e}")       # e is small 
f.close()

Solving this challenge was more of a learning and discovery. While I immediately recognized that this was a problem that should be solved by CRT, the regular method for calculating CRT which is given below, did not work. It errored out in the step where the product of the modulii is inverted with respect to a modulus.

def crt(n, a):
    sum = 0
    prod = reduce(lambda a,b: a*b, n)

    for n_i, a_i in zip(n, a):
        print(f"checking ... {n_i} and {a_i}")
        p = prod // n_i
        sum += a_i * gmpy2.invert(p, n_i) * p       # <---- not invertible error here 
    return sum % prod

Researching this problem some more led me to the cause of the error (which is that the modulii are NOT co-prime to each other) and there is a more robust version of the CRT implementation that would handle this scenario.

Here is a fantastic explanation of the theory and the background of how this strong version of the CRT works. I will not try to duplicate that explanation here. You should go and read it there.

Sage and Sympy handles this scenario already. So, an easier way to solve this challenge is to use those library functions. However, I wanted to understand the mechanics of CRT and implement it from first principles. So, the final solution is:

def lcm(numbers):
    return reduce(lambda x, y: x * y // gcd(x, y), numbers, 1)

def egcd(a, b):
    if a == 0:
        return (0, 1, b)
    else:
        y, x, g = egcd(b % a, a)
        return (x - (b // a) * y, y, g)
    
def crt_strong(n, a):
    assert len(n) == len(a)
    n0 = n[0]
    a0 = a[0]

    for i in range(1,len(n)):
        ni = n[i]
        ai = a[i]

        g = gcd(ni, n0)
        if (ai % g != a0 %g):
            print("Error ... no solution")
            return None

        u,v,mygcd = egcd(n0//g, ni//g)
        mod = (n0//g) * ni

        x = (a0 * (ni//g) * v + ai * (n0//g) * u) % mod 
        while(x < 0):
            x += mod
        a0 = x 
        n0 = mod
    return (a0, n0)   

N = []
R = []
e = 3
with open('output.txt', 'r') as F:
    for i in range(7):
        l = F.readline().strip().split(' ')
        N.append(int(l[4]))     # modulus
        R.append(int(l[6]))     # residual := CT^3 % modulus

# print pair-wise GCD to show that moduli are not co-prime 
print("\nGCD Matrix ... pair-wise GCD of all modulus values\n")
for i in range(len(N)):
    for j in range(len(N)):
        if (i != j):
            print(f"{gcd(N[i], N[j]):5d}", end = '')
        else: 
            print(f"    -", end = '')
    print('')
print('')

# the strong version of CRT accounts for modulii that are not pairwise co-prime 
m_cubed, L = crt_strong(N, R)   # Call Sage's crt() method automatically does this, so does sympy's crt() method
m,found = gmpy2.iroot(m_cubed, e)
print(found, long_to_bytes(m))  # True b'flag{Wh4t_d0_y0u_m34n_1t_h4s_t0_b3_co-pr1m3}'

'''
# Sympy implementation
from sympy.ntheory.modular import crt
from sympy import cbrt
print(long_to_bytes(cbrt(crt(N, R)[0])))

# Sage implementation 
f = crt(R, N)
print(ltb(ZZ(f).nth_root(3)))
'''

Knapsack

This is a classic Knapsack subset problem. In this mode, given a set of values in the ‘knapsack’ you can choose each item either 0 or 1 times exactly once to create a subset sum of a given value. The intent in this challenge is to determine the sequence of 1s and 0s to form a binary value that form the basis of the encryption key.

I tried to solve this with LLL, but it failed due to the density of the matrix being too high (density approx = 1.1). This is the Meet in the middle approach to solving this challenge.

from collections import defaultdict
import hashlib
from Crypto.Util.number import long_to_bytes
from Crypto.Cipher import AES

# Given 
c='af95a58f4fbab33cd98f2bfcdcd19a101c04232ac6e8f7e9b705b942be9707b66ac0e62ed38f14046d1cd86b133ebda9'
nums    =[600848253359, 617370603129, 506919465064, 218995773533, 831016169202, 501743312177, 15915022145, 902217876313, 16106924577, 339484425400, 
          372255158657, 612977795139, 755932592051, 188931588244, 266379866558, 661628157071, 428027838199, 929094803770, 917715204448, 103431741147, 
          549163664804, 398306592361, 442876575930, 641158284784, 492384131229, 524027495955, 232203211652, 213223394430, 322608432478, 721091079509, 
          518513918024, 397397503488, 62846154328, 725196249396, 443022485079, 547194537747, 348150826751, 522851553238, 421636467374, 12712949979]
subset  = 7929089016814

# dictionary for each half of the iterations.  Key -> subset sum, Value -> list of values (bit masks) that produced the subset
left_dict = defaultdict(list)
right_dict = defaultdict(list)

def decrypt_cipher(c, bitmask):
    secret = long_to_bytes(int(bitmask, 2))         # b'atTS4'
    print(f"{bitmask=} | {int(bitmask,2)} | {secret=}")
    key = hashlib.sha256(secret).digest()[:16]
    cipher = AES.new(key, AES.MODE_ECB)
    return cipher.decrypt(bytes.fromhex(c))

for i in range(2**20):
    left = [nums[20+x]  if (i & 1<<x) else 0 for x in range(20)]
    left_dict[sum(left)].append(i)

    right = [nums[x] if (i & 1<<x) else 0 for x in range(20)]
    right_dict[sum(right)].append(i)

    # for testing ---    
    # if (bin(i).count('1') == 1):
    #    print(f"{i:6d} {left} {right} = {sum(left)+sum(right):15d}")
    
# matching logic, for each sum in the left dictionary, see if there is a complement on the other dictionary, so that together they add up to the required subset
for lsum in left_dict.keys():
    if (subset - lsum) in right_dict.keys():
        left_bits = f"{left_dict[lsum][0]:020b}"            # one half of the bit mask
        right_bits = f"{right_dict[subset-lsum][0]:020b}"   # the other half
        print(f"Match found {left_bits} + {right_bits}")
        exit(decrypt_cipher(c, left_bits + right_bits ))    #b'flag{N0t_r34dy_f0r_M3rkl3-H3llman}\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00'

Forensics

Forenscript

It's thundering outside and you are you at your desk having solved 4 forensics challenges so far. Just pray to god you solve this one. You might want to know that sometimes too much curiosity hides the flag.

We are given a binary file a.bin. Using XXD to dump the file shows that it might be a PNG image file, but the header chunks look wonky. Also, the entire file is not reversed but smaller pieces of it. By examining the first 12-16 bytes, we can see the pattern - every four bytes of the PNG file have been reversed. So, we need to undo this transformation.

% xxd a.bin | more
00000000: 474e 5089 0a1a 0a0d 0d00 0000 5244 4849  GNP.........RDHI
00000010: 460c 0000 a504 0000 0000 0608 3dab 1f00  F...........=...
...

# print as hex, take 8 chars (4 bytes), reverse their positions, assemble into one long hex, convert it back to binary, store as a.png
% xxd -c4 -p a.bin | sed -E 's/(..)(..)(..)(..)/\4\3\2\1/g' | tr -d '\n' | xxd -r -p > a.png

# viewing this image shows a message stating `FAKE FLAG`. So, there is another layer to this onion

% binwalk a.png 
DECIMAL       HEXADECIMAL     DESCRIPTION
--------------------------------------------------------------------------------
0             0x0             PNG image, 3142 x 1189, 8-bit/color RGBA, non-interlaced
91            0x5B            Zlib compressed data, compressed
60048         0xEA90          PNG image, 3142 x 1189, 8-bit/color RGBA, non-interlaced
60139         0xEAEB          Zlib compressed data, compressed

# we can see that there is another PNG image starting at offset=60048. Let's extract it.

% dd if=a.png of=b.png ibs=1 skip=60048 
% file b.png
b.png: PNG image data, 3142 x 1189, 8-bit/color RGBA, non-interlaced

# Opening this new image gives us the flag  flag{scr1pt1ng_r34lly_t0ugh_a4n't_1t??}

So, in retrospect, we can solve this challenge with a single bash command pipeline.

% xxd -c4 -p a.bin | sed -E 's/(..)(..)(..)(..)/\4\3\2\1/g' | tr -d '\n' | xxd -r -p | dd skip=60048 of=b.png ibs=1
# open b.png and get the flag

Drunk

I solved this challenge after the CTF. We are given a encoded file that looks like a base64 string along with a text file with what looks to be octal or decimal characters. I guess the fact that the key looked to be in base64, seems to indicate that it was a Fernet encryption scheme.

Fernet (symmetric encryption) - looks like base64 but decodes to garbage, in two parts. First part (32 bytes) is the key. Uses 128-bit AES in CBC mode and PKCS7 padding, with HMAC using SHA256 for authentication. IV is created from os.random(). ¹

% printf "$(sed -e 's/^/\\/' -e 's/ /\\/g' something.txt)" | xxd -r -p | base64 -d
zlMg5K3TobbFh_8l7doDT_408rH7Md_W3Oc1yKX1FrA=  # <--- use this as the key

Decode the encoded.bin file with the key.

from cryptography.fernet import Fernet

f = Fernet('zlMg5K3TobbFh_8l7doDT_408rH7Md_W3Oc1yKX1FrA=')
output = f.decrypt(open('encoded.bin', 'r').readline())
print(f"{len(output)} bytes decrypted")
p = open('drunk.png', 'wb')
p.write(output)
p.close()

The resulting drunk.png has the flag.

Resources

Challenges

Category	Challenge	Description
Beginner	Beginner-menace
Beginner	Cheat Code
Beginner	Escape The Room
Beginner	Fruit Basket
Beginner	Headache
Beginner	Indecipherable-image-or-is-it?
Beginner	Marks
Beginner	Not So Guessy
Beginner	Secret-of-Kurama
Beginner	Something_in_Common
Beginner	mini_RSA_v2
Beginner	mini_RSA
Beginner	secret_of_j4ck4l
Blockchain	BabyBlackjack
Blockchain	VulnChain
Crypto	ColL3g10n
Crypto	Curvy_Curves
Crypto	Knapsack
Crypto	PRSA
Crypto	ProveMeWrong
Crypto	Rebellious
Crypto	Safe Curvy Curve
Crypto	Secure_Matrix_Transmissions_v2
Crypto	Secure_Matrix_Transmissions
FeedBack	Feedback Form
Forensics	Drunk
Forensics	Forenscript
Forensics	Sonic-Hide_and-Seek
Forensics	The Shakespearean Mouse
Misc	halo-jack again
Misc	halo-jack
Rev	Blowcode
Rev	Gotta Go Fast
Rev	Hiashi of the shades
Rev	Open Sesame
Rev	Secret Door
Rev	Sl4ydroid
Rev	baby eBPF
pwn	Baby Formatter
pwn	EmpDB
pwn	Konsolidator
pwn	Master Formatter v2
pwn	Master Formatter
pwn	Pizzeria
web	Rocket Explorer
web	Unintelligible-Chatbot
web	armoured-notes
web	php_sucks
web	space-war
web	too-many-admins

https://zweilosec.gitbook.io/hackers-rest/os-agnostic/cryptography-and-encryption ↩︎

Beginner¶

Mini RSA¶

Mini RSA_v2¶

Indecipherable-image-or-is-it?¶

Crypto¶

Something in Common¶

Knapsack¶

Forensics¶

Forenscript¶

Drunk¶

Resources¶

Challenges¶