Wargames.my CTF 2023 | CTF notepad

A CTF organized by a team from Malaysia. It was a tidy little event with some interesting challenges.

Crypto

N-less RSA

This is a RSA challenge with unknown N, but we have the totient function phi(n). We are also provided the logic used to determine the private primes p and q.

def generate_secure_primes():
	p = getStrongPrime(1024)
	q = int(next_prime(p*13-37*0xcafebabe))
	return p,q

# Generate two large and secure prime numbers
p,q = generate_secure_primes()
n = p*q
e = 0x10001
phi = (p-1)*(q-1)
c = pow(bytes_to_long(flag),e,n)

# we are given phi, e and c, but not n

Given that we have phi and the relationship between p and q, we can solve for them using any of the following three methods.

Method 1: By factoring phi

# Use https://www.alpertron.com.ar/ECM.HTM to factor phi

from Crypto.Util.number import isPrime, long_to_bytes
from itertools import combinations
from functools import reduce


phi=340577739943302989719266782993735388309601832841016828686908999285012058530245805484748627329704139660173847425945160209180457321640204169512394827638011632306948785371994403007162635069343890640834477848338513291328321869076466503121338131643337897699133626182018407919166459719722436289514139437666592605970785141028842985108396221727683676279586155612945405799488550847950427003696307451671161762595060053112199628695991211895821814191763549926078643283870094478487353620765318396817109504580775042655552744298269080426470735712833027091210437312338074255871034468366218998780550658136080613292844182216509397934480
e=65537
ct=42363396533514892337794168740335890147978814270714150292304680028514711494019233652215720372759517148247019429253856607405178460072049996513931921948067945946086278782910016494966199807084840772350780861440737097778578207929043800432279437709296060384506082883401105820800844187947410153745248466533960754243807208804084908637481187348394987532434982032302570226378255458486161579167482667571132674473067323283939026297508548130085016660893371076973067425309491443342096329853486075971866389182944671697660246503465740169215121081002338163263904954365965203570590704089906222868145676419033148652705335290006075758484

factors = [2,2,2,2,5,17,23,127,34883,64327,31855469,41906999093,103832676376161046043,
42928682841447187075836289855892629156535900514107927517684293084786844441409957297894592527460787241683614840492974772427636887719994128565592152980944126724469079274172144474672062412412603584793646346956898729686409791648474545298852872995161295471414165954724402947,
6420760786362823769296653774296236632402429318675915367452603711386456193709958608737754568883471330653872083531628632121784399208909036073963921230370375260817560046504060944356316155772191086712627421688528565251967757404295337261653707746185260317688974197060087034705221140112831521071507609
]

print(len(factors))
# Work out which combination (product) of factors produce possible values for P-1 and Q-1
for n in range(1, len(factors)):
    comb = combinations(factors, n)
    print(f"testing [C({n})]...")
    for c in comb:
        prod = reduce(int.__mul__, c)
        # find the product of all the factors and see if it is 1 less than a prime number
        if isPrime(prod+1) and isPrime(phi//prod+1):
            p = prod+1
            q = phi//(p-1) + 1
            d = pow(e, -1, phi)
            pt = pow(ct, d, p*q)
            m = long_to_bytes(pt)
            # print(m.decode())
            if b"wgmy" in m:
                exit(m.decode())

Method 2: Bruteforce + quadratic roots to determine p

from Crypto.Util.number import long_to_bytes

F.<p> = ZZ[]

# given 
phi=340577739943302989719266782993735388309601832841016828686908999285012058530245805484748627329704139660173847425945160209180457321640204169512394827638011632306948785371994403007162635069343890640834477848338513291328321869076466503121338131643337897699133626182018407919166459719722436289514139437666592605970785141028842985108396221727683676279586155612945405799488550847950427003696307451671161762595060053112199628695991211895821814191763549926078643283870094478487353620765318396817109504580775042655552744298269080426470735712833027091210437312338074255871034468366218998780550658136080613292844182216509397934480
e=65537
c=42363396533514892337794168740335890147978814270714150292304680028514711494019233652215720372759517148247019429253856607405178460072049996513931921948067945946086278782910016494966199807084840772350780861440737097778578207929043800432279437709296060384506082883401105820800844187947410153745248466533960754243807208804084908637481187348394987532434982032302570226378255458486161579167482667571132674473067323283939026297508548130085016660893371076973067425309491443342096329853486075971866389182944671697660246503465740169215121081002338163263904954365965203570590704089906222868145676419033148652705335290006075758484

for i in range(1000):
    f = (p - 1) * (p*13-37*0xcafebabe + i) - phi
    if (len(f.roots()) != 0):
        p = f.roots()[0][0]
        q = phi // (p - 1) + 1
        assert phi % (p - 1) == 0
        assert phi % (q - 1) == 0

        n = p * q
        d = pow(e, -1, phi)
        m = pow(c, d, n)
        print(long_to_bytes(m))
        break

Method 3: Z3 solver

from z3 import *
from Crypto.Util.number import long_to_bytes

# given 
phi=340577739943302989719266782993735388309601832841016828686908999285012058530245805484748627329704139660173847425945160209180457321640204169512394827638011632306948785371994403007162635069343890640834477848338513291328321869076466503121338131643337897699133626182018407919166459719722436289514139437666592605970785141028842985108396221727683676279586155612945405799488550847950427003696307451671161762595060053112199628695991211895821814191763549926078643283870094478487353620765318396817109504580775042655552744298269080426470735712833027091210437312338074255871034468366218998780550658136080613292844182216509397934480
e=65537
c=42363396533514892337794168740335890147978814270714150292304680028514711494019233652215720372759517148247019429253856607405178460072049996513931921948067945946086278782910016494966199807084840772350780861440737097778578207929043800432279437709296060384506082883401105820800844187947410153745248466533960754243807208804084908637481187348394987532434982032302570226378255458486161579167482667571132674473067323283939026297508548130085016660893371076973067425309491443342096329853486075971866389182944671697660246503465740169215121081002338163263904954365965203570590704089906222868145676419033148652705335290006075758484

p = Int('p')
q = Int('q')
incr = Int('incr')

s = Solver()
s.add((p-1) * (q-1) == phi)
s.add(q == (p*13-37*0xcafebabe + incr))
# set the boundary conditions p, q and incr all should be positive integers
s.add(p > 0)
s.add(q > 0)
s.add(incr > 0)
# set an upper bound to `incr` as the nextPrime() should find one close to the start value (13p - k)
s.add(incr < 1000)  # tune as needed.

if s.check() == sat:
    m = s.model()
    P = m[p].as_long()
    Q = m[q].as_long()
    N = P*Q
    print(f'Found Solution: \n{P =}\n{Q =}')

    d = pow(e, -1, phi)
    print(long_to_bytes(pow(c, d, N)))      # b'wgmy{a9722440198c2abad490478875be2815}'
else:
    print('Unsat :(')

Method 4:

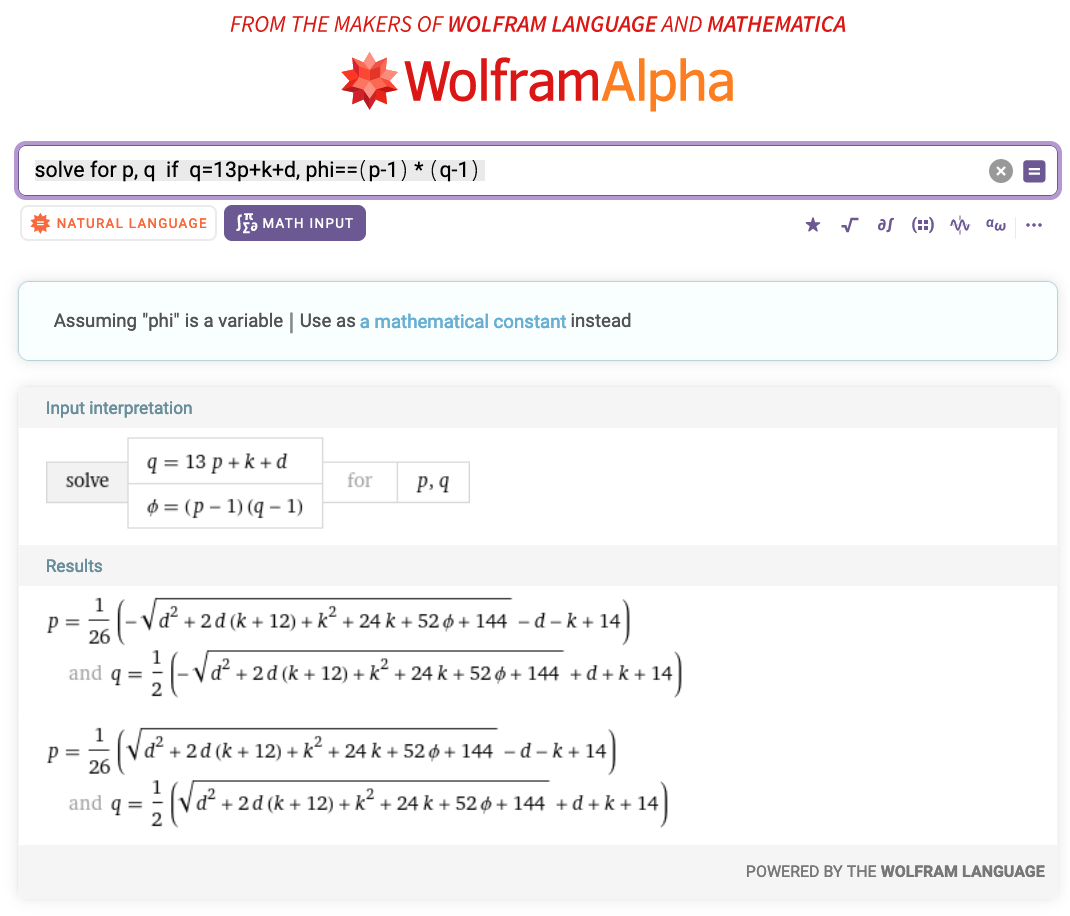
from Crypto.Util.number import long_to_bytes
# given 
phi=340577739943302989719266782993735388309601832841016828686908999285012058530245805484748627329704139660173847425945160209180457321640204169512394827638011632306948785371994403007162635069343890640834477848338513291328321869076466503121338131643337897699133626182018407919166459719722436289514139437666592605970785141028842985108396221727683676279586155612945405799488550847950427003696307451671161762595060053112199628695991211895821814191763549926078643283870094478487353620765318396817109504580775042655552744298269080426470735712833027091210437312338074255871034468366218998780550658136080613292844182216509397934480
e=65537
c=42363396533514892337794168740335890147978814270714150292304680028514711494019233652215720372759517148247019429253856607405178460072049996513931921948067945946086278782910016494966199807084840772350780861440737097778578207929043800432279437709296060384506082883401105820800844187947410153745248466533960754243807208804084908637481187348394987532434982032302570226378255458486161579167482667571132674473067323283939026297508548130085016660893371076973067425309491443342096329853486075971866389182944671697660246503465740169215121081002338163263904954365965203570590704089906222868145676419033148652705335290006075758484

k = -37*0xcafebabe
d = 0
while True:
    q = ( sqrt(d^2 + 2*d*(k+12) + k^2 + 24*k + 52*phi + 144) +d +k +14)/2
    if q in ZZ:
        break
    d += 1
p = (phi/(q-1)) +1
n = p*q
d = pow(e, -1, phi)
print(long_to_bytes(pow(c,d,n)))

Ho Ho Ho 2

Want to make a wish for this Christmas? Submit here and we will tell Santa!!

1. Register
2. Login
3. Make a wish
4. Wishlist (Santa Only)
5. Exit
Enter option: 1
Enter your name: aaaaaa
Use this token to login: 6076a84d0f90efbfb4a2ddc7a3f1436f

To solve this challenge, we need to login with the name with Santa Claus in it and have a valid token.

The token generator is a LCG with just one randomly generated value

m = 0xb00ce3d162f598b408e9a0f64b815b2f
a = 0xaaa87c7c30adc1dcd06573702b126d0d
c = 0xcaacf9ebce1cdf5649126bc06e69a5bb
n = getRandomNBitInteger(64)

def generateToken(name):
	x = bytes_to_long(name.encode(errors="surrogateescape"))
    # LCG fast skip implementation
    # is equivalent to the following code
    # for _ in range(n):
    # 	x = (a*x + c) % m
	x = ((pow(a, n, (a-1)*m) - 1) // (a-1) * c + pow(a, n, m) * x) % m
	return hex(x)[2:]

The algorithm for the fast skip LCG calculation is explained very well at this site.

$$ Token \quad T = \overbrace{[[x\cdot a + c]\cdot a + c] \cdots + c]]}^{\text{nested n-times}}\\ T = x\cdot a^n + c\cdot a^{n-1}+ c\cdot a^{n-2}+ \cdots + c \\ T = x\cdot a^n + c\cdot ( a^{n-1} + a^{n-2} + \cdots + 1 ) \\ T = x\cdot a^n + c\cdot (\dfrac{a^n-1}{a-1}) \pmod{m}\\ \space \\ \text {Given x, m, a, c and T, calculate n}\\ \space \\ T \cdot {(a-1)} = x\cdot{a^n}\cdot{(a-1)} + c\cdot{a^n} - c\\ T \cdot {(a-1)}+c = x\cdot{(a-1)}\cdot{a^n} + c\cdot{a^n}\\ T\cdot{(a-1)}+c = {a^n}\cdot{(x\cdot{(a-1)} + c)} \\ {a^n} = \dfrac{ T\cdot{(a-1)}+c}{x\cdot{(a-1)} + c}\\ \space \\ {n} = {log_a} \Big[ \dfrac{ T\cdot{(a-1)}+c}{x\cdot{(a-1)} + c} \Big] \pmod {m} \space \\ \space \\ \text {In Sage, use the following equation and simplify to solve for } a^n \\ T = x\cdot a^n + c\cdot (\dfrac{a^n-1}{a-1}) \pmod{m}\\ x\cdot a^n + c\cdot (\dfrac{a^n-1}{a-1}) - T =0 \pmod{m}\\ $$

The full solution is:

from pwn import *
from Crypto.Util.number import bytes_to_long

def regUser(R, username):
    R.recvuntil(b'Enter option:')
    R.sendline(b'1')
    R.recvuntil(b'name:')
    R.sendline(username)
    R.recvuntil(b'to login:')
    t = R.recvline().strip()
    return t

R = process(['python3', 'hohoho1-server.py'])
# R = remote('',)

context.log_level = 'debug'

uname = b'aaaaaaaa'
t = regUser(R, uname)
print(f"{uname}  --> {t}")
m = 0xb00ce3d162f598b408e9a0f64b815b2f
a = 0xaaa87c7c30adc1dcd06573702b126d0d
c = 0xcaacf9ebce1cdf5649126bc06e69a5bb

T = int(t, 16)
x = bytes_to_long(uname)
# `p` is the variable to represent a**n
#  T = a^n x + c (a^n - 1)/(a-1)
#  a^n (is not xor)
F.<p> = Zmod(m)[]
f = p*x + c * (p - 1) / (a - 1) - T
print(f"Simplified equation: {f = } = 0")
lst = f.coefficients()
an = (-lst[0]) / lst[1]

print(f"Coeff {lst = }\n {an = }")
# Find discrete log with base `a` to get `n`
n = int(an.log(a))
print(f"Found {n = }")

def generateToken(name):
	x = bytes_to_long(name.encode(errors="surrogateescape"))
	x = ((pow(a, n, (a-1)*m) - 1) // (a-1) * c + pow(a, n, m) * x) % m
	return hex(x)[2:]

# Generate a token for `Santa` using our calculated value for `n`
santa_token = generateToken('Santa Claus')

# Use the self-generated token to login as Santa
R.recvuntil(b'Enter option:')
R.sendline(b'2')
R.recvuntil(b'name:')
R.sendline(b'Santa Claus')
R.recvuntil(b'token:')
R.sendline(santa_token)

# Use option 4 to view the wishlist and get the flag
R.interactive()

Forensic

See You

We are given a PCAP file with the instructions that one the machines was found to be exfiltrating information. Wireshark’s protocol statistics show a bunch of TLS traffic (which we can ignore) and some UDP traffic. A large portion of the UDP traffic comes from port 38884.

% tshark -r artifact.pcapng -z io,phs
#<snip>
===================================================================
Protocol Hierarchy Statistics
Filter: 

eth                                      frames:21247 bytes:23866862
  ip                                     frames:21227 bytes:23865225
    udp                                  frames:18993 bytes:1295197
      data                               frames:18351 bytes:1248704
      dns                                frames:236 bytes:24597
      mdns                               frames:8 bytes:712
      llmnr                              frames:1 bytes:67
      jmirror                            frames:23 bytes:1817
        ipv6                             frames:22 bytes:1748
          _ws.malformed                  frames:19 bytes:1476
          data                           frames:2 bytes:182
        ip                               frames:1 bytes:69
          _ws.malformed                  frames:1 bytes:69
      ssdp                               frames:18 bytes:3766
      dhcp                               frames:2 bytes:666
    tcp                                  frames:2231 bytes:22569848
      tls                                frames:823 bytes:21959388
        tcp.segments                     frames:527 bytes:20067651
          tls                            frames:510 bytes:20007994
      http                               frames:36 bytes:12865
        data-text-lines                  frames:11 bytes:6776
    igmp                                 frames:3 bytes:180
  ipv6                                   frames:12 bytes:1229
    icmpv6                               frames:3 bytes:270
    udp                                  frames:9 bytes:959
      mdns                               frames:8 bytes:872
      llmnr                              frames:1 bytes:87
  arp                                    frames:8 bytes:408
===================================================================

% tshark -r artifact.pcapng -Y 'udp.srcport == 38884' -T fields -e 'udp.dstport' | cut -c 3- | awk '{printf "%c",$0}' | xxd 
00000000: 8950 4e47 0d0a 1a0a 0000 000d 4948 4452  .PNG........IHDR
00000010: 0000 0376 0000 0110 0802 0000 0073 fd71  ...v.........s.q
00000020: b400 0000 0173 5247 4200 aece 1ce9 0000  .....sRGB.......
# <snip>
% tshark -r artifact.pcapng -Y 'udp.srcport == 38884' -T fields -e 'udp.dstport' |                  
                            # ^^ Read the PCAP file, filter by udp source port == 38884, and extract only the UDP target port
cut -c 3- |                 # ignore the first 2 digits and capture the rest
awk '{printf "%02x",$0}' |  # Convert from decimal to hex
xxd -r -p > cu.png          # convert from hex string to byte values and store it as 'cu.png'

Open the resulting image file to read the flag.

References & Writeups

Challenges

Category	Challenge	Description
CRYPTO	Hohoho 2 Continue
CRYPTO	Hohoho 2
CRYPTO	N-less RSA
FORENSIC	Can’t Snoop
FORENSIC	Compromised
FORENSIC	SeeYou
MISC	Dialect
MISC	Sayur
MISC	Splice
MISC	Warmup - Game
OTHER	Feedback Form
PPC	Linux Memory Usage
PPC	Lokami Temple
PWN	Free Juice
PWN	Magic Door
PWN	Pak Mat Burger
REVERSE	Defeat the boss!
REVERSE	RmRf
WEB	My First AI Project
WEB	Pet Store Viewer
WEB	Report Google?
WEB	Secret
WEB	Status
WEB	Truco
WEB	Warmup - Web
WEB	myCloud

Crypto¶

N-less RSA¶

Ho Ho Ho 2¶

Forensic¶

See You¶

References & Writeups¶

Challenges¶