This CTF was organized by the University of Texas, Austin’s Info Security association. I participated as part of the team Weak But Leet and we were placed 9th out of approximately 900 teams participating.
Here are some of the challenges I solved and the approach I took.
Crypto
RSA 256
 We are given the following values for this RSA based challenge.
We are given the following values for this RSA based challenge.
N = 77483692467084448965814418730866278616923517800664484047176015901835675610073
e = 65537
c = 43711206624343807006656378470987868686365943634542525258065694164173101323321
N seems to be incredibly small. We can see that it can be factored easily.
from math import gcd
from Crypto.Util.number import long_to_bytes, inverse
from factordb.factordb import FactorDB
N = 77483692467084448965814418730866278616923517800664484047176015901835675610073
e = 65537
c = 43711206624343807006656378470987868686365943634542525258065694164173101323321
def decrypt(ct, e, p, q):
phi = (p-1)*(q-1)
d = inverse(e, phi)
return long_to_bytes(pow(ct, d, p*q))
f = FactorDB(N)
f.connect()
p, q = f.get_factor_list()
print(p, q)
print(decrypt(c, e, p, q)) #b'utflag{just_send_plaintext}'
Numbers go brrr …
This challenge uses a randomly generated seed to derive the key for a AES based encryption. We are given an opportunity to encrypt any text of our choice and are also provided the encrypted flag using the same key scheme (not the same key). Since the search space for the seed is small (1e6), it is quite trivial to bruteforce it. We just need to be careful to reconstruct the number of calls to encrypt() so that the state of the seed is properly set for the next operation.
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad
from pwn import *
possible_seeds = [x for x in range(10 ** 6)]
seed = 0
my_string = b"ABCDEFGHabcdefgh"
encrypted_vals = {}
def get_random_number():
global seed
seed = int(str(seed * seed).zfill(12)[3:9])
return seed
def encrypt(message):
key = b''
for i in range(8):
key += (get_random_number() % (2 ** 16)).to_bytes(2, 'big')
cipher = AES.new(key, AES.MODE_ECB)
ciphertext = cipher.encrypt(pad(message, AES.block_size))
return ciphertext.hex()
def decrypt(message):
key = b''
for i in range(8):
key += (get_random_number() % (2 ** 16)).to_bytes(2, 'big')
cipher = AES.new(key, AES.MODE_ECB)
pt = cipher.decrypt(unhex(message))
return pt
P = remote('betta.utctf.live', 7356)
# P = process (['python3','main.py'])
P.recvuntil(b'2 - encrypt a message)?')
P.sendline(b'2') # encrypt a message
P.recvuntil(b'your message?')
P.sendline(my_string)
P.recvuntil(b'encrypted message: ')
E = P.recvline().strip().decode()
P.recvuntil(b'2 - encrypt a message)?')
P.sendline(b'1') # get encrypted flag
P.recvuntil(b'encrypted flag: ')
F = P.recvline().strip().decode()
# E = '801fa795bdee61bc65ac606d1ca1dad81dc9a4e7e39116ec24185edaa32e3026'
# F = '4ae905d3eee4a7228ba5007f4ac185c7ab88124e5d6726e3b000ad4b6db654348bf7a95f6837b4a2dcf73138aa5834e0'
print(f"{my_string} --> {E}")
print(f"{F=}")
# brute force the seed
for s in possible_seeds:
seed = s
enc = encrypt(my_string)
if (enc == E):
print(s, enc)
seed = s # reset the seed
print("My string --> ",decrypt(E))
print("Flag: ")
exit(decrypt(F))
if (s %10000 == 0):
print(f"{s}")
Running against the server with our chosen text retrieves the seed. We then use it to decrypt the flag.
% python3 solve_brrr.py
[+] Opening connection to betta.utctf.live on port 7356: Done
b'ABCDEFGHabcdefgh' --> 92beb658211b567309b7c0c6bf1e3e0bedb1bca2db4bb2bdfa2b9fad85833662
F='7ccf8fb3bb1c88a5c1f748b1185a0de85ddd642452f690ebaa99b284792de0b1f3278e95b651200de33ca5b9c67d6572'
0
10000
20000
30000
40000
43337 92beb658211b567309b7c0c6bf1e3e0bedb1bca2db4bb2bdfa2b9fad85833662
My string --> b'ABCDEFGHabcdefgh\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10'
Flag:
b'utflag{deep_seated_and_recurring_self-doubts}\x03\x03\x03'
[*] Closed connection to betta.utctf.live port 7356
Numbers go brrr 2 …
Bits and pieces
Another RSA based challenge. We are given three sets of n, e and c. The chosen values of modulus are not cryptographically secure and can be easily overcome.
from math import gcd
from Crypto.Util.number import long_to_bytes, inverse
from factordb.factordb import FactorDB
n1=16895844090302140592659203092326754397916615877156418083775983326567262857434286784352755691231372524046947817027609871339779052340298851455825343914565349651333283551138205456284824077873043013595313773956794816682958706482754685120090750397747015038669047713101397337825418638859770626618854997324831793483659910322937454178396049671348919161991562332828398316094938835561259917841140366936226953293604869404280861112141284704018480497443189808649594222983536682286615023646284397886256209485789545675225329069539408667982428192470430204799653602931007107335558965120815430420898506688511671241705574335613090682013
e1=65537
c1=7818321254750334008379589501292325137682074322887683915464861106561934924365660251934320703022566522347141167914364318838415147127470950035180892461318743733126352087505518644388733527228841614726465965063829798897019439281915857574681062185664885100301873341937972872093168047018772766147350521571412432577721606426701002748739547026207569446359265024200993747841661884692928926039185964274224841237045619928248330951699007619244530879692563852129885323775823816451787955743942968401187507702618237082254283484203161006940664144806744142758756632646039371103714891470816121641325719797534020540250766889785919814382
n2=22160567763948492895090996477047180485455524932702696697570991168736807463988465318899280678030104758714228331712868417831523511943197686617200545714707332594532611440360591874484774459472586464202240208125663048882939144024375040954148333792401257005790372881106262295967972148685076689432551379850079201234407868804450612865472429316169948404048708078383285810578598637431494164050174843806035033795105585543061957794162099125273596995686952118842090801867908842775373362066408634559153339824637727686109642585264413233583449179272399592842009933883647300090091041520319428330663770540635256486617825262149407200317
e2=65537
c2=19690520754051173647211685164072637555800784045910293368304706863370317909953687036313142136905145035923461684882237012444470624603324950525342723531350867347220681870482876998144413576696234307889695564386378507641438147676387327512816972488162619290220067572175960616418052216207456516160477378246666363877325851823689429475469383672825775159901117234555363911938490115559955086071530659273866145507400856136591391884526718884267990093630051614232280554396776513566245029154917966361698708629039129727327128483243363394841238956869151344974086425362274696045998136718784402364220587942046822063205137520791363319144
n3=30411521910612406343993844830038303042143033746292579505901870953143975096282414718336718528037226099433670922614061664943892535514165683437199134278311973454116349060301041910849566746140890727885805721657086881479617492719586633881232556353366139554061188176830768575643015098049227964483233358203790768451798571704097416317067159175992894745746804122229684121275771877235870287805477152050742436672871552080666302532175003523693101768152753770024596485981429603734379784791055870925138803002395176578318147445903935688821423158926063921552282638439035914577171715576836189246536239295484699682522744627111615899081
e3=65537
c3=17407076170882273876432597038388758264230617761068651657734759714156681119134231664293550430901872572856333330745780794113236587515588367725879684954488698153571665447141528395185542787913364717776209909588729447283115651585815847333568874548696816813748100515388820080812467785181990042664564706242879424162602753729028187519433639583471983065246575409341038859576101783940398158000236250734758549527625716150775997198493235465480875148169558815498752869321570202908633179473348243670372581519248414555681834596365572626822309814663046580083035403339576751500705695598043247593357230327746709126221695232509039271637
def decrypt(ct, e, p, q):
phi = (p-1)*(q-1)
d = inverse(e, phi)
return long_to_bytes(pow(ct, d, p*q))
# the first modulus can easily be factored using FactorDB
f = FactorDB(n1)
f.connect()
p1, q1 = f.get_factor_list()
# Modulus 2 and 3 share a prime factor. Use GCD to determine the factor and its complement.
p23 = gcd(n2, n3)
q2 = n2 // p23
q3 = n3 // p23
pt = bytearray(decrypt(c1, e1, p1, q1))
pt.extend(decrypt(c2, e2, p23, q2))
pt.extend(decrypt(c3, e3, p23, q3))
print(pt.decode())
# utflag{oh_no_it_didnt_work_</3_i_guess_i_can_just_use_standard_libraries_in_the_future}
Cryptordle
This challenge has a game of wordle, where you are given 6 tries to guess a 5-character word. With each guess, you are given some information about correctly placed letters. In this mathematical equivalent of the challenge, the information provided is the product of the difference between the letters of the guessed word and the answer, taken to modulo 31.
The approach I took was to develop an oracle of the responses for 5 consistent guesses and record the sequence of responses for each of the words in the wordle list (taken from https://github.com/pythonmcpi/wordle-wordlist/blob/main/wordlist.txt). Since this list only contains 2239 words, it was quite trivial to calculate the response and store them for lookup. Then, we connect to the server, send that exact sequence of 5 canned guesses, capture the responses and lookup the original word from the list. Doing this three times will earn us the flag.
from pwn import *
lookups = defaultdict(list)
def calc_response(guess, offset=0):
ans = 1
for i in range(5):
ans = (ans * (-1*guess[i] + offset + i)) % 31
return ans
def calc_response_series(solution):
guess = [ord(c)-ord('a') for c in solution]
answers = [calc_response(guess, x) for x in range(5)]
# print(f"{guess} -> {answers} --> {solution}")
str_ans = str(answers)
lookups[str_ans].append(solution)
# Wordle wordlist from https://github.com/pythonmcpi/wordle-wordlist/blob/main/wordlist.txt
W = open('wordle.txt', 'r')
words = W.read().strip().split('\n')
for w in words:
calc_response_series(w)
print(f"Precalculated words: {len(lookups)}")
#P = process(["python3", "cryptordle_2.py"])
P = remote('betta.utctf.live', 7496)
canned = [b'abcde', b'bcdef', b'cdefg', b'defgh', b'efghi']
for iter in range(3):
responses = []
for attempts in range(5):
P.recvuntil(b"guess?\n")
P.sendline(canned[attempts])
responses.append(int(P.recvline().strip()))
str_ans = str(responses)
print(f"looking up ... {str_ans} ... {lookups[str_ans]}")
my_answer = lookups[str_ans][0]
P.recvuntil(b'guess?\n')
P.sendline(my_answer.encode())
guess_response = P.recvline().strip()
print(guess_response)
P.interactive()
% python3 solve_cryptordle.py
Precalculated words: 2263
[+] Opening connection to betta.utctf.live on port 7496: Done
looking up ... [0, 10, 22, 25, 10] ... ['suite']
b'Good job! Onward...'
looking up ... [24, 0, 20, 7, 24] ... ['wooer']
b'Good job! Onward...'
looking up ... [17, 10, 27, 7, 24] ... ['gamut']
b'Good job! Onward...'
[*] Switching to interactive mode
Nice! You got it :) Have a flag:
utflag{sometimes_pure_guessing_is_the_strat}
On discord, Minh_AT20A (minhack) shared their brilliant solution, which does not require the use of the wordlist. I tried to describe their solution and my analysis of it here.
Let the secret word have its characters at an index of \( [w_1,w_2,w_3,w_4,w_5]\). These indices are with respect to the letter a being at 0. So, the word apple would be represented as \( [0, 15, 15, 11, 4]\). Our challenge is to determine these indices given the responses from the server, which happens to be \( \prod (g_i-w_i) \mod 31 \), where \(g_i\) is the guessed letter and \(w_i\) is the actual letter.
For each word, we will try 5 guesses. With the guesses being aaaaa, baaaa, abaaa, aabaa and aaaba.
For the first guess, aaaaa, the response from the server is
$$
\begin{align}
r_1 &= ( 0 - w_1 ) * ( 0 - w_2 ) * ( 0 - w_3 ) * ( 0 - w_4 ) * ( 0 - w_5 ) \notag \\
r_1 &= - (w_1 \cdot w_2 \cdot w_3 \cdot w_4 \cdot w_5 ) \pmod {31} \\
\end{align}
$$
For the second guess, baaaa, the response from the server is
$$
\begin{align}
r_2 &= ( 1 - w_1 ) * ( 0 - w_2 ) * ( 0 - w_3 ) * ( 0 - w_4 ) * ( 0 - w_5 ) \notag \\
r_2 &= (w_2 \cdot w_3 \cdot w_4 \cdot w_5) - (w_1 \cdot w_2 \cdot w_3 \cdot w_4 \cdot w_5 ) \pmod {31} \\
r_1 - r_2 &= - (w_2 \cdot w_3 \cdot w_4 \cdot w_5) \pmod {31} \\
\frac {r_1} {r_1 - r_2} &= w_1 \pmod {31} \\
Likewise, \notag \\
\frac {r_1} {r_1 - r_3} &= w_2 \pmod {31} \\
\frac {r_1} {r_1 - r_4} &= w_3 \pmod {31} \\
\frac {r_1} {r_1 - r_5} &= w_4 \pmod {31} \\
\\
Finally, \notag \\
w_5 &= \frac {- r_1} {w_1 \cdot w_2 \cdot w_3 \cdot w_4} \pmod {31} \\
\end{align}
$$
Since we are doing modular arithmetic, all division above should be represented as $$ \frac {a} {b} \pmod {n} = a * b^{-1} \pmod {n} \\ \text{In python, } a * pow(b, -1, n) \pmod {n} $$
The only catch with the above solution is that if the secret word contains the letter a, \(r_1 = 0\) and one of \(r_2,r_3,r_4,r_5 = 0\). This causes the pow() function to fail, producing the base is not invertible for the given modulus error.
def calc_answer(r):
ans = []
product = -1
for i in range(1, 5):
ans.append((r[0] * pow(r[0] - r[i], -1, 31)) % 31)
product *= ans[-1]
ans.append( (r[0] * pow(product, -1, 31)) % 31 )
return ''.join[chr(ord('a')+x) for x in ans]
P = remote('betta.utctf.live', 7496)
canned = [b'aaaaa', b'baaaa', b'abaaa', b'aabaa', b'aaaba']
for iter in range(3):
responses = []
for attempts in range(5):
P.recvuntil(b"guess?\n")
P.sendline(canned[attempts])
responses.append(int(P.recvline().strip()))
my_answer = calculate_answer(responses)
P.recvuntil(b'guess?\n')
P.sendline(my_answer.encode())
guess_response = P.recvline().strip()
print(guess_response)
P.interactive()
simple signature
This is a simple challenge that tests our understanding of modular arithmatics. We are just given the server information. No source code is provided. Essentially, the server implements textbook RSA encryption oracle. In the discovery stage, the Oracle provides a signature (encrypted value) for any message we provide. In the challenge stage, we are asked to predict the signature for a message that was not used in the discovery stage.
We can take advantage of the property \( a \mod n * b \mod n = (a * b) \mod n \).
So if we use 2 and 3 as the messages and get their corresponding signatures, we can multipy them to get the signature of 6. You could also use just 2 and predict 4 or any other power using the same approach.
% nc betta.utctf.live 4374
Welcome to the signature generator!
This service generates signatures for nonnegative integer messages.
Today's RSA parameters are:
n = 17007115661299815607779165325006475925060995570648249126487030335644203023481846638117502461440332111444430916767200503666795042264359564422897594202938598017705990008042877313795222435128369842652331645057052654864153662402967586505198149442619066069665399964917886690584407737138071046442779048899209367834725450164047862000686231313652343200922838123212694312780180541822058518287645925643501380574048457140971384357731590128868557198143735637246158985421310165371697896791564736610273577022563266299497980201341938025773037378412970953178288939570091648227422253383650988673431907753115858499383009001338523288087
e = 65537
Enter a message as an integer (enter 0 to stop): 2
Your signature is: 6672957953572898291912874637593697014101172364647215740830900911644569712185295765745418452963497463275123251748952403305001368745981830456197804415177494270001131898055965726185773582177908222725950920241045612464232492749961514337999947924777746096071879416722777928572833948616707226872981090448612762382663274986788162021813367382415915672886879690116171900002788502748187211138753302953634267728098740540801330595107303819427658290454721300644156991165726094646851144048881902055363646383706901609234926756120255588681727697911438036366466679519130986883486700046862967465455783444359689098389239391853331493149
Enter a message as an integer (enter 0 to stop): 3
Your signature is: 2489355093949788277772248629243069986608791937535601737135622933254496365765932518220438140785809898088376102226248195015617328688580982151381273120828016088777408113045970326379287582105630891959710381877864144955748352250386354887117900428266230023602707106952578855774464713335240514344219988834753712048133975681621557356736836815344888196103902767834383982656310862090337589073425432345749789501727668558023522752244962712971711970202489196742528339273279883755796908964160428004572278447515065391236485876470418430841869466382073943825117186740672592574369890018680015742556388573397785190613698745962915695490
Enter a message as an integer (enter 0 to stop): 0
Now, come up with your own pair!
Enter a message: 6
Enter a signature: 14071926959502352328380108893612792408930849940054769138731539539797284861381027564760805034456674079194751849440050601008224090587555734474642565439947816573139566057142197638959372821291461186224771449119199402392012619783441779586295184695621428676659073013109298875136062352474750406101619288057300425450550330323130832272063150985860276007537835351448157112351580410138120126218032966787106781425709270942254627926303136136674377015196131322660751367363551425575897100657913517435897399704928026360474015505014191516023064743653631124181763466586472824010087247361266453912366414029602415895092188782055670958869
Congrats! Here is the flag: utflag{a1m05t_t3xtb00k_3x3rc153}
Forensics
Gibberish

This was probably the most frustrating of the challenges in this CTF. Yes, even more than Insanity. First things first. We are given a PCAP file, that seems to contain USB HID traffic. Exploring the data for a while gives us the source address and the fields of interest.
% tshark -r keyboard.pcapng -T fields -e frame.time_epoch -e usbhid.data -Y "usb.src == 1.13.1"
...
1711740183.168567000 0000000000000000 Example showing 6 keys being pressed simultaneously
1711740191.173510000 0000040000000000
1711740191.306985000 0000040800000000
1711740191.365781000 0000040806000000
1711740191.553956000 0000040806110000
1711740191.558936000 0000040806111000
1711740191.715559000 0000040806111033 [MODIFIERS][00][K1][K2][K3][K4][K5][K6]
1711740191.878911000 0000040811103300
1711740191.889882000 0000081110330000
1711740191.900091000 0000111033000000
1711740191.926066000 0000111000000000
1711740191.947494000 0000110000000000
1711740191.949953000 0000000000000000
...
We know that USBHID key values will need to tranlated according to the appropriate keyboard layout, as well as to account for the modifier keys (control, shift, alt) being added.
from pwn import *
# USB keyboard HID key codes
usb_codes = {
0x04:['a','A'], 0x05:['b','B'], 0x06:['c','C'], 0x07:['d','D'], 0x08:['e','E'], 0x09:['f','F'],
0x0A:['g','G'], 0x0B:['h','H'], 0x0C:['i','I'], 0x0D:['j','J'], 0x0E:['k','K'], 0x0F:['l','L'],
0x10:['m','M'], 0x11:['n','N'], 0x12:['o','O'], 0x13:['p','P'], 0x14:['q','Q'], 0x15:['r','R'],
0x16:['s','S'], 0x17:['t','T'], 0x18:['u','U'], 0x19:['v','V'], 0x1A:['w','W'], 0x1B:['x','X'],
0x1C:['y','Y'], 0x1D:['z','Z'], 0x1E:['1','!'], 0x1F:['2','@'], 0x20:['3','#'], 0x21:['4','$'],
0x22:['5','%'], 0x23:['6','^'], 0x24:['7','&'], 0x25:['8','*'], 0x26:['9','('], 0x27:['0',')'],
0x28:['\n','\n'], 0x29:['[ESC]','[ESC]'], 0x2A:['⌫','⌫'], 0x2B:['\t','\t'],
0x2C:[' ',' '], 0x2D:['-','_'], 0x2E:['=','+'], 0x2F:['[','{'], 0x30:[']','}'], 0x31:['\',"|'],
0x32:['#','~'], 0x33:";:", 0x34:"'\"", 0x36:",<", 0x37:".>", 0x38:"/?",
0x39:['[CAPSLOCK]','[CAPSLOCK]'], 0x3A:['F1'], 0x3B:['F2'], 0x3C:['F3'], 0x3D:['F4'], 0x3E:['F5'],
0x3F:['F6'], 0x41:['F7'], 0x42:['F8'], 0x43:['F9'], 0x44:['F10'], 0x45:['F11'],
0x46:['F12'], 0x4f:[u'→',u'→'], 0x50:[u'←',u'←'], 0x51:[u'↓',u'↓'], 0x52:[u'↑',u'↑']
}
# tshark -r keyboard.pcapng -T fields -e frame.time_epoch -e usbhid.data -Y "usb.src == 1.13.1" > hid_data.txt
# 1711739472.285762000 00001a0000000000
F = open('hid_data.txt', 'r').readlines()
old_ts = 0.0
prev_keys = []
key_sequence = []
key_batch = []
for line in F:
ts, keys = line.strip().split('\t')
ts = float(ts)
delta = ts - old_ts
keys = unhex(keys)
shifted = 0
# Detect if Shift is pressed
if (keys[0] & 0x22 > 0 ):
shifted = 1
assert keys[1] == 0x00
pressed_keys = []
for i in range(2,8):
if keys[i] != 0x0:
pressed_keys.append(usb_codes[keys[i]][shifted])
print(f"{delta:.4f} : {pressed_keys}")
if (len(pressed_keys) == 0):
# find the longest series and store it
if (len(key_batch) > 0):
k = max(key_batch, key=len)
key_sequence.append(k)
key_batch.clear()
else:
key_batch.append(''.join(pressed_keys))
old_ts = ts
prev_keys = pressed_keys
S = ''.join(key_sequence)
print('\n'.join(key_sequence))
At this point, I was stumped as to what the keystrokes might mean. In an attempt to analyze the alphabet, I generated a frequency distribution of the letters.
% fold -w 1 keystrokes_in.txt | sort | uniq -c | sort
1 ]
1 h
4 '
6
9 u
10 l
11 g
17 o
17 s
26 k
27 ;
27 [
31 d
43 f
44 m
46 w
48 e
48 i
49 a
52 r
64 j
66 c
70 v
72 n
76 p
263 ⌫
My teammate recognized that there are no b, z or t being used and surmised that it could be stenography. A quick search of “stenography on qwerty” produced a number of hits on Plover, OpenStenography and other similar sites. A check on the OpenStenography site with some of the key combos quickly confirmed that it is indeed stenography. So, the next step was to find out which keys go together. To determine this we pulled in the time_epoch field from the usb capture and calculated the difference between the keystrokes.
The following sequence shows the key sequence fgmik[ being recorded.
DELAY : KEYS
0.0272 : [] < no keys pressed
7.8514 : ['f'] < keys started to be held
0.0404 : ['f', 'g']
0.0340 : ['f', 'g', 'm']
0.0516 : ['f', 'g', 'm', 'i']
0.0105 : ['f', 'g', 'm', 'i', 'k']
0.3199 : ['f', 'g', 'm', 'i', 'k', '['] < 6 keys simultaneously held down >
0.1880 : ['g', 'm', 'i', 'k', '['] < keys being released>
0.0006 : ['m', 'i', 'k', '[']
0.2700 : ['m', 'i', 'k']
0.0415 : ['m', 'i']
0.0020 : ['m']
0.0018 : [] < all keys are released>
14.8371 : ['w'] < next sequence starts after a noticeable gap>
For each batch, the longest sequence of keys is assumed to be the pertinent one and we store it. Using Plover and with a lot of guesswork, we determine that the following set of keystrokes are the ones corresponding to the flag. After battling with Plover some more, I tried another way. I saw that Plover had a rich suite of test cases.
def test_gibberish(capture, machine, strokes):
machine.start_capture()
ks = ["anp","wercfl","wv","mp","wecrfl","weflkp","rfnjik","fgikm[","awervl","wenm","fgikm[","vik","fgikm[","cnm","fgikm[","sdjnp","sdfnm","fgmik[","svcnk[","fgmik[","a","fgikm[","sdvcnm","sdvcnm","fgmik[","mnuop[","wefgk"]
for k in ks:
s = ' '.join([c for c in k])
send_input(capture, s)
print(f"{s} --> {strokes}")
capture.reset_mock()
del strokes[:]
assert 1 == 1
I added another test case using the same framework and fed our keystrokes and converted them into stenographical text. For example, the keystrokes m p gives us u t. So, doing this for the keystrokes of interest gives us the Steno equivalents for the QWERTY text entered.
% pytest -s test_keyboard.py
======================================== test session starts ========================================
platform darwin -- Python 3.10.12, pytest-8.1.1, pluggy-1.4.0
rootdir:
configfile: pytest.ini
plugins: anyio-3.6.2
collected 7 items
test_keyboard.py ...
a n p --> [{'S-'}, {'-E'}, {'-T'}] --> set
w e r c f l --> [{'T-'}, {'P-'}, {'H-'}, {'A-'}, {'R-'}, {'-G'}] --> flag
w v --> [{'T-'}, {'O-'}] --> to
m p --> [{'-U'}, {'-T'}] --> ut
w e c r f l --> [{'T-'}, {'P-'}, {'A-'}, {'H-'}, {'R-'}, {'-G'}] --> flag
w e f l k p --> [{'T-'}, {'P-'}, {'R-'}, {'-G'}, {'-B'}, {'-T'}] --> {
r f n j i k --> [{'H-'}, {'R-'}, {'-E'}, {'-R'}, {'-P'}, {'-B'}] --> learning
f g i k m [ --> [{'R-'}, {'*'}, {'-P'}, {'-B'}, {'-U'}, {'-D'}] --> _
a w e r v l --> [{'S-'}, {'T-'}, {'P-'}, {'H-'}, {'O-'}, {'-G'}] --> stenog (??)
w e n m --> [{'T-'}, {'P-'}, {'-E'}, {'-U'}] --> raphy (??)
f g i k m [ --> [{'R-'}, {'*'}, {'-P'}, {'-B'}, {'-U'}, {'-D'}] --> _
v i k --> [{'O-'}, {'-P'}, {'-B'}] --> on
f g i k m [ --> [{'R-'}, {'*'}, {'-P'}, {'-B'}, {'-U'}, {'-D'}] --> _
c n m --> [{'A-'}, {'-E'}, {'-U'}] --> a
f g i k m [ --> [{'R-'}, {'*'}, {'-P'}, {'-B'}, {'-U'}, {'-D'}] --> _
s d j n p --> [{'K-'}, {'W-'}, {'-R'}, {'-E'}, {'-T'}] --> qwerty
s d f n m --> [{'K-'}, {'W-'}, {'R-'}, {'-E'}, {'-U'}] --> qwerty
f g m i k [ --> [{'R-'}, {'*'}, {'-U'}, {'-P'}, {'-B'}, {'-D'}] --> _
s v c n k [ --> [{'K-'}, {'O-'}, {'A-'}, {'-E'}, {'-B'}, {'-D'}] --> keyboard
f g m i k [ --> [{'R-'}, {'*'}, {'-U'}, {'-P'}, {'-B'}, {'-D'}] --> _
a --> [{'S-'}] --> is
f g i k m [ --> [{'R-'}, {'*'}, {'-P'}, {'-B'}, {'-U'}, {'-D'}] --> _
s d v c n m --> [{'K-'}, {'W-'}, {'O-'}, {'A-'}, {'-E'}, {'-U'}] --> [deleted]
s d v c n m --> [{'K-'}, {'W-'}, {'O-'}, {'A-'}, {'-E'}, {'-U'}] --> quite
f g m i k [ --> [{'R-'}, {'*'}, {'-U'}, {'-P'}, {'-B'}, {'-D'}] --> _
m n u o p [ --> [{'-U'}, {'-E'}, {'-F'}, {'-L'}, {'-T'}, {'-D'}] --> difficult
w e f g k --> [{'T-'}, {'P-'}, {'R-'}, {'*'}, {'-B'}] --> }
....
The next step was to use a lot of guesswork intelligence to read the steno text to have it make sense, while referencing the online resources to lookup values for symbols and punctuations. For example R*PBUD is the underscore character.
This site was incredibly useful to guess decode the steno text into normal english.
utflag{learning_stenography_on_a_qwerty_keyboard_is_quite_difficult}
PS: after discussing with the challenge author, I realized that I overlooked something important. The usbhid.data field can identify only 6 keys (as it has room for only 6 bytes). However, some of the chords use a key combo of longer than 6 keys. This is recognized by key strokes where some keys are released and new keys are pressed, without the keyboard being idle. The following is an example of such a scenario, showing a chord of ecrnmkl
0.1055 : []
11.6665 : ['e']
0.0895 : ['e', 'c']
0.0130 : ['e', 'c', 'r']
0.1145 : ['e', 'c', 'r', 'n']
0.0499 : ['e', 'c', 'r', 'n', 'm']
0.2860 : ['e', 'r', 'n', 'm']
0.0091 : ['e', 'n', 'm']
0.0030 : ['n', 'm']
0.2325 : ['n', 'm', 'k']
0.1845 : ['n', 'm', 'k', 'l']
0.2780 : ['n', 'm', 'k']
0.0028 : ['n', 'm']
0.0382 : []
Insanity Check: Reimagined

A teammate discovered that the favicon for the http://utctf.live/ site seemed to have some interesting information. Digging into it a bit more, we can see that the SVG file has logic for animations. The SVG file itself is pretty cool. It changes colors slowly with the color gradient lightening and darkening over time. However, you can manipulate the parameters for the center object to speed up the animation and we can see it blinks in a non-uniform manner. Looking closely at the animation code, we can see that the percentage values and the color codes for the fill seem to be of interest.
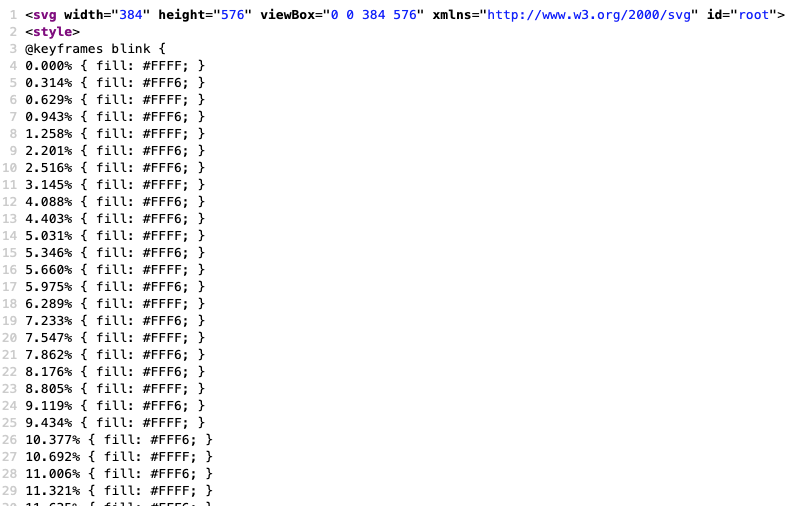
Let’s extract it into a file to process it later.
% grep "fill:" favicon.svg | sed -e 's/ {/,/g' -e 's/ fill: #//g' -e 's/; }//g' | tr -d %
0.000,FFFF
0.314,FFF6
0.629,FFFF
0.943,FFF6
1.258,FFFF
2.201,FFF6
2.516,FFF6
...
# save to a text file and process with python
% grep "fill:" favicon.svg | sed -e 's/ {/,/g' -e 's/ fill: #//g' -e 's/; }//g' | tr -d % > favicon_data.txt
Next we calculate the difference between progress values in each row. And, for sure it seems to be uneven. Charting these delays shows that there is a clear pattern of what appears to be morse code.

A close up view of the first word shows the scheme used.
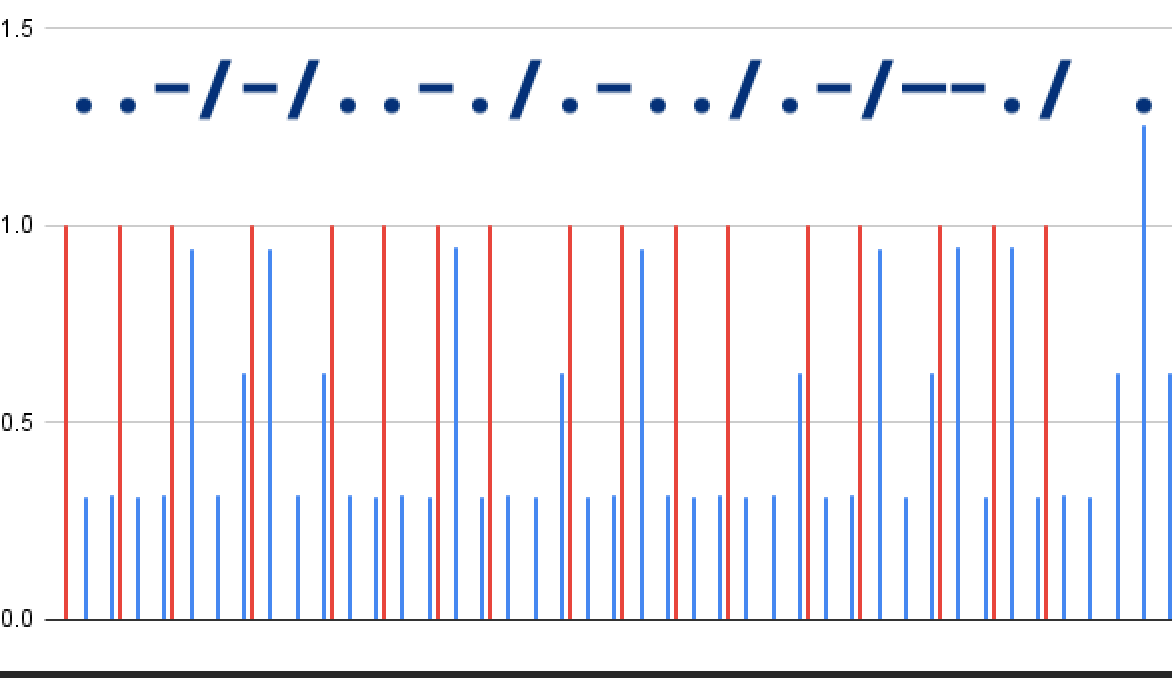
~ 0.3 0.3 -> dot
~ 0.9 0.3 -> dash
~ 0.6 -> end of symbol
~ 1.2 -> Space, end of word
While we can visually decode the morse code, I wanted to save whatever little bit of sanity left in me and wrote the following quick and dirty python script to extract the morse code.
def translate(delta):
ans = ''
if (delta < 0.4): # short
ans += '.'
elif (delta > 1.0): # space, eow
ans += ':'
elif (delta > 0.8): # long
ans += '-'
else:
ans += '/' # end of symbol
return ans
'''
favicon_data.txt
0.000,FFFF
0.314,FFF6
0.629,FFFF
0.943,FFF6
'''
morse = ""
F = open('favicon_data.txt', 'r').readlines()
old_ts = 0
for line in F:
ts, val = line.split(',')
val = val.strip() # not used
ts = float(ts)
delta = ts - old_ts
print(f"{val} --> {delta:.2f}")
if (delta > 0):
morse += translate(delta)
old_ts = ts
# short delay + short delay = dot, long delay + short delay = dash
morse = morse.replace("..", '.').replace("-.", "-")
print(morse)
# ..-/-/..-./.-../.-/--./:/..-/-/-.-./-/..-./:/..-/..././.../:/.../...-/--./:/-/---/:/../-/.../:/..-./..-/.-../.-.././.../-/::
# UTFLAG UTCTF USES SVG TO ITS FULLEST
# utflag{utctf_uses_svg_to_its_fullest}
Resources
- http://www.openstenoproject.org/
- http://www.openstenoproject.org/plover/
- https://spectra.sammdot.ca/
- https://connor-mccartney.github.io/cryptography/other/UTCTF-2024
- https://warlocksmurf.github.io/posts/utctf2024/
- https://seall.dev/posts/utctf2024
- https://hackmd.io/@benjaminion/bls12-381#Rogue-key-attacks (Forgery)
- https://ctf.krauq.com/utctf-2024
- https://slefforge.github.io/CTF.html
Challenges
Category Challenge Description Binary Exploitation E-Corp Binary Exploitation Handwritten Webserver Cryptography Beginner: Anti-dcode.fr Cryptography Cryptordle Cryptography Forgery Cryptography RSA-256 Cryptography bits and pieces Cryptography numbers go brrr 2 Cryptography numbers go brrr Cryptography simple signature Forensics A Very Professional Website Forensics Contracts Forensics Gibberish Forensics Insanity Check: Reimagined Forensics OSINT 1 Forensics OSINT 2 Forensics OSINT 3 Forensics Study Music Misc CCV Misc Survey Reverse Engineering Accelerated Hell Reverse Engineering Beginner: Basic Reversing Problem Reverse Engineering Fruit Deals Reverse Engineering In The Dark Reverse Engineering PES-128 Web Beginner: Off-Brand Cookie Clicker Web Easy Mergers v0.1 Web Home on the Range Web Schrödinger Web Unsound
